魔方学院免广告 v2.2.25 安卓版

魔方学院版，是佛山市计客创新科技有限公司打造的一款3D魔方教学平台。魔方这一玩具，从小孩到大人都颇为流行，直至现在，依旧是众多小朋友钟爱的玩具。它不仅趣味性十足，还能锻炼大家的思维能力。看似平平无奇，只是一个普通正方体模样的魔方，却因那数个正方形色块，被赋予了独特的魅力。

魔方学院版本，借助强大算法助力你还原魔方。其提供的解法步骤清晰，你只需跟着视频操作，就能轻松上手。该版本会带你从最基础的解法入手，深入了解魔方玩法，让你在短时间内还原魔方，毫无压力！

软件特色

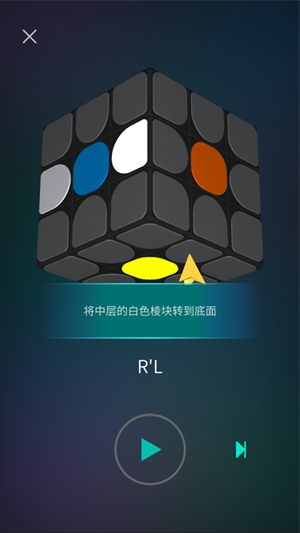
1）填色快解：智能识别状态，逐步帮你还原魔方

任意打乱状态自动识别并计算出三十步左右还原步骤，原创转动面引导，轻松跟走，零基础也能快速还原魔方。

2）花式图案：魔方的创意玩法，拼出各式魔方花样

挑选你喜欢的魔方图案，根据填色的魔方状态，生成解法，跟走拼出对应的花式。

3）新手教程：精美3D动画引导，哪里不会点哪里

根据手上魔方情况选择观看相应的动画演示，记录学习进度，一步一步真正学会还原魔方。

4）计时功能：还原魔方快不快，赶紧计时来看看

支持自由计时和生成打乱公式，记录你学习魔方路上进步的点点滴滴。

软件功能

1、【填色功能】

用户根据手上魔方色块状况，点击软件端3D魔方填色，实现同步功能

2、【3D动画演示功能】

提供3D动画演示功能，具备自动播放与分步骤播放两种选择方式。

3、【情景选择功能】

提供魔方3D动画教程，用户根据实际遇到的情况，选择点击对应的教程动画观看

4、【进度标识功能】

提供关卡式设置，自动标记观看学习进度，完成本关卡学习即可解锁下一个关卡

5、【装备解锁功能模块】

支持解锁不同种类魔方装备、分阶段关卡、智能游戏玩法、魔方装备个性化设置

魔方学院版使用方法

1、进入软件，点击选择几阶魔方

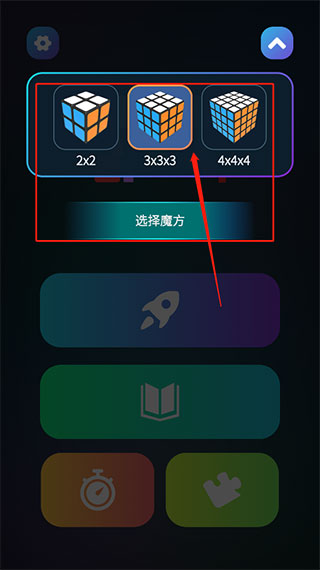
2. 轻点这个代表火箭发射的按钮

3、将自己手中魔方的颜色一个个点击上去

4、点击完成之后魔方会一步步进行处理，用户只需要跟着操作就行

魔方学院版还原技巧

8355法

8355法，由中国台湾许技江（Reheart Sheu）发明，方法与层先法类似，但是公式量更少。

步骤：6步；公式量：3个；平均还原步数：100+。

基本思路是首先还原底面十字，然后是复原底层三个角块，第四个角块不还原，而是利用此空槽来还原三个中层棱块和三个顶层棱块。下一步是还原剩下的两个棱块。最后一步是反复使用公式RUR’U’来还原剩下的五个角块。

8：和LBL法类似，将第一层完成，只是刻意留下一个角没解开，留做“工作区(Working Area)”

3：利用工作区将第二层的3 个边塞入，不像LBL法需要背两个镜向动作的“八步法”

5：利用工作区将顶层与工作区的5 个边归位，不像LBL法需要背“六步法”以及两个镜象OLL公式

5：此时剩下顶层与工作区的5 个角，利用简单的去返动作，即可达到位置送换，以及翻动方向，此时一颗方块即解答完成。

桥式法

桥式法（Roux Method），由Gilles Roux于2003年发明。是一种即简单易学，又可以取得非常优秀的成绩的方法。

步骤数量：4步；公式数量范围：9 - 42；平均还原步数：约50步。

还原思路是先在左侧做一个1x2x3的块，再在右侧做一个1x2x3的块。留下顶层和竖着的中层可以自由转动。下一步是还原顶层4个角块的方向和位置，最后一步是仅仅通过转动U和M来还原余下的六个棱块和四个中心块(6E4C)。该方法可以说是速拧还原中步数最短的方法，但是由于其转动有较多M层转动，不是非常适合最少步的还原。

CFOP

Fridrich Method（简称CFOP），最初由David Singmaster、René Schoof、Jessica Fridrich、Hans Dockhorn、Anneke Treep等人各自贡献了不同部分的思路，经由Jessica Fridrich在1981年整理补充公式并就此流传开来。

步骤：4步；公式量：119个；平均还原步数：55左右。

CFOP本质是层先法的变种，但是由于其归纳出了可能出现的各种情况，所以在记忆量上面要增大许多倍（119个公式），但同时也能有效的增加速度。

把底层转出一个与色块分布相符的十字（Cross）

同时将底层角块和相对应棱块归位 （F2L，First 2 Layers） ，41个公式

最上层利用公式将颜色统一 （OLL，Orientation of Last Layer），57个公式

将最上层侧面的颜色统一 （PLL，Permutation of Last Layer），21个公式

现在绝大多数魔方高手都使用Fridrich Method，因为相对于它能达到的速度来说，119个公式的记忆量就显得不多了。

CFCE

CFCE由Guus Razoux Schultz发明，其与CFOP同时代被发明提出。

具体步骤为4步，涉及的公式数量达112个，平均还原步数约54步。

CFCE的具体思路和CFOP相近，前两步都是顶面十字以及前两层。第三步通过一步公式来还原所有顶面角块的方向与位置（CLL），最后一步则是还原顶层所有棱块的方向与位置（ELL）。